Distanta De La Punct La Dreapta In Spatiu

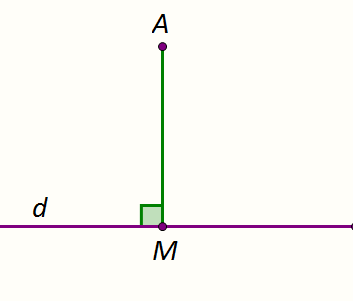
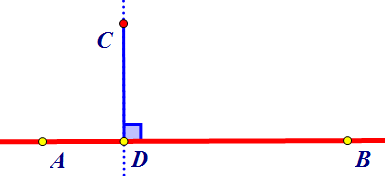
știm că distanța de la un punct la o dreaptă este lungimea dintre acel punct și piciorul perpendicularei de pe dreaptă dusă din acel punct.
Distanta de la punct la dreapta in spatiu. O formulă pentru a calcula această distanță va fi dată în cele ce urmează. Fie punctul m x m y m si dreapta d de ecuatie. Distanta de la un punct m 0 la o dreapta d în spatiu. Atunci distanta de la punctul m 0 la dreapta d este.
Dupa cum se stie distanta de la punctul m la dreapta d este data de distanta de la punctul m la proiectia sa m pe d vezi figura. Ax by c 0. Conditia de coliniaritate a 3 puncte. Unde este vectorul director al dreptei d.
Fie și dreapta. Se noteaza cu literele mari ale alfabetului. Fie dreapta d m 0 d m 1 x 1 y 1 z 1 proiectia lui m 0 x 0 y 0 z 0 pe dreapta d. Determinantul de ordin mai mic decat 4.
Distanta de la un punct la o dreapta. Presupunem pentru a trata cazul general ca a 0 b 0 si panta dreptei d fiind conform celor de mai sus o perpendiculara pe ea va avea panta. Distanța de la un punct la o dreaptă. Intersectia a doua drepte determina un punct.
Punctul punctul poate fi comparat cu urma lasata de creion pe hartie. Produsul vectorial a. Distanța de la un punct la o dreaptă. A b c punctul nu are dimensiuni.
Distanta de la un punct la o dreapta determinanti.