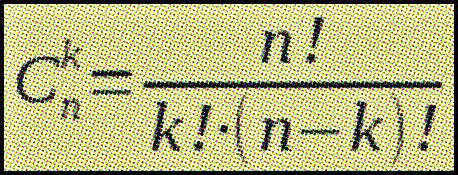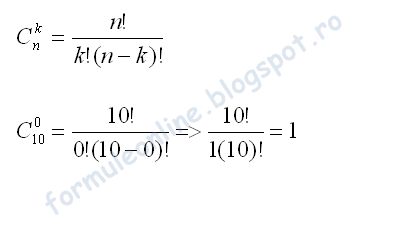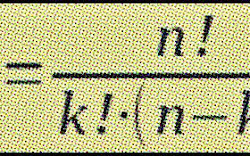Combinari De N Luate Cate K Formula Excel

C n n 2 n.

Combinari de n luate cate k formula excel. Combinari de n luate cate k si rezulta exercitii rezolvate combinari calculator combinari. Numărul combinărilor de n luate câte k este. Combinări de n luate câte k matematică pentru începători. Permutari aranjamente combinari analiza combinatorica pe intelesul tau clasa 10 duration.

Combinatorica este ramura matematicii care se ocupă în principal cu numărarea modurilor în care pot fi alese anumite obiecte respectând anumite condiții. C n k n. C n n b n. și vom vedea mai jos de ce.

A b n c n 0 a n c n 1 a n 1 b c n 2 a n 2 b 2. Ckn cn kn c n k c n n k. în acest articol voi prezenta cele trei elemente de bază ale combinatoricii precum și câteva aplicații ale acestora. C de n luate cate k n k.

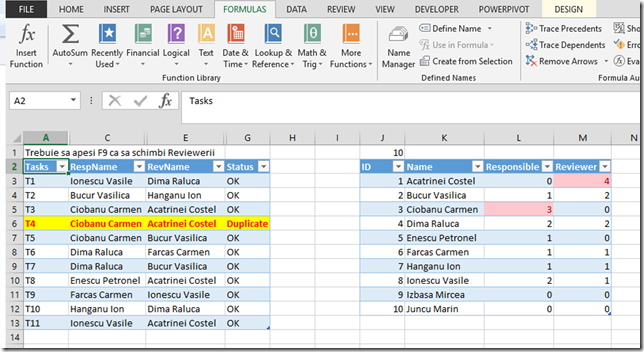
N 49 numarul total de bile k 6 numarul de bile ce pot fi extrase rezultat 13 983 816 variante posibile formula si modul de calcul pas cu pas exercitii rezolvate combinari. De exemplu dacă cineva o să vă întrebe câte submulțimi de câte două elemente se pot forma cu elemente furate dintr o mulțime care are patru elemente atunci voi le veți putea răspunde că numărul căutat este combinări de patru luate câte doi și veți scrie el este egal cu șase. A b ϵ r n ϵ n termenul general de rang k 1. Dacă a este o mulțime cu n elemente unde n n atunci submulțimile lui a formate fiecare din k elemente 0 k n se numesc combinări de n elemente luate câte k.

Combinările reprezintă numărul tuturor submulțimilor de k elemente ale unei mulțimi cu n elemente. C n k c n n k. Ckn ckn 1 ck 1n 1 c n k c n 1 k c n 1 k 1. Akn k 0 k n n k ϵ n c n k n.

E si f se fac folosind formula. Se aplica formula combinarilor. T k 1 c n k a n k b k. Andreea trebuie sa aplici formula combinarilor de n luate cate k in cazul particular k 1.

C n 0 c n 1. A n k k 0 k n n k ϵ n. Exerciții rezolvate bac permutări. Numărul combinărilor de n elemente luate câte k este.

A n k k 0 k n n k ϵ n. C n k c n 1 k c n 1 k 1. C n k a n k b k. Combinari de n luate cate k n k combinari de n 1 luate cate k 1 k 1 n 1 combinari de n 1.

O să revin cu alte exerciții rezolvate.