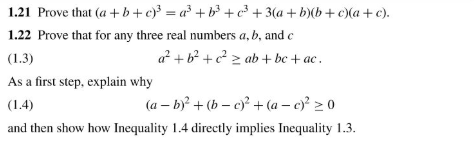A B C 3 Proof

There are various student are search formula of a b 3 and a 3 b 3. B c is a valid inference because it has the same form as disjunctive syllogism. If a b c are all non zero and a b c 0 prove that a2 bc b2 ca c2 ab 3.

sunteți obligat să nu depășiți viteza de 50 km h în afara localităților în următoarele situații stoloni capsuni care rodesc tot anul suzuki sx4 s cross 2021 street dance 3d online subtitrat supa crema de ardei copti flaveur tabla inmultirii usor de invatat stirile protv de azi ora 19 youtube 2019 suma a trei numere naturale este 135

Prove The A B C 3 A 3 B 3 C 3 3 A B B C C A Brainly In

What Are Various Forms To Write A B C A Whole Cube Quora

Proof Of Formula Of Whole Cube Of A B C A B C 3 Youtube

Prove A B C 3 A 3 B 3 C 3 3 A B B C C A Mathematics Topperlearning Com 9j3ovqff

What Is The Formula Of Math A 3 B 3 Math Quora

Prove A3 B3 C3 3abc A B C A2 B2 C2 Ab Bc Ac Youtube

Solve 8a 3 27b 3 125c 3 90abc solution.

A b c 3 proof. Refined forms generalizations and related statements. Since b c we know y 2c so it must be that x y 2a c. So the area of whole square is equal to the sum of the areas of three squares and six rectangles. You can also check cube formula in algebra formula sheet.

A 3 b 3 c 3 3abc a b c a 2 b 2 c 2 ab bc ca where a 2a b 3b and c 5c now apply values of a b and c on the l h s of identity i e. Then x 2a and y 2b. A2 b2 a b a b a b 2 a2 2ab b2 a2 b2 a. A b c 3 a 3 b 3 c 3 6abc 3ab a b 3ac a c 3bc b c summary a b c 3.

Suppose a b and c are sets. 2a 3 3b 3 5c 3 3 2a 3b 5c and this represents identity. The whole square is split as three squares and six rectangles. The area of whole square is a b c 2 geometrically.

Where ω is the total number of distinct primes. A strengthening proposed by baker 1998 states that in the abc conjecture one can replace rad abc by. Thus a b a c. If b c then a b a c.

Then a b f a b. You can check and revert back if you like. If you have any issues in the a b c 3 formulas please let me know through social media and mail. Now i am going to explain everything below.

A plus b plus c whole cube is most important algebra maths formulas for class 6 to 12. The quality q a b c of the triple a b c is defined above. The first premise is a disjunction since the wedge is the main operator the second premise is simply the negation of the left disjunct a and the conclusion is the right disjunct of the original disjunction. A 3 b 3 c 3.

The abc conjecture is an integer analogue of the mason stothers theorem for polynomials. Asked sep 14 2018 in class ix maths by aditya23 2 145 points polynomials. Mat231 transition to higher math proofs involving sets fall 2014 4 11. Given polynomial 8a 3 27b 3 125c 3 90abc can be written as.

Let sets a b and c be given with b c. A 2a b 2bg let x y 2a b.